Topzle Topzle

Knight's tour

Updated: Wikipedia source

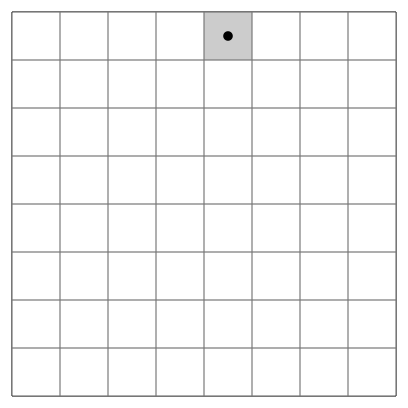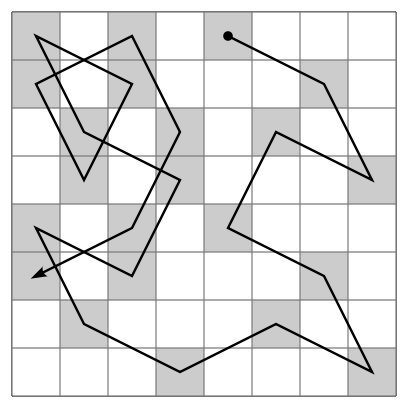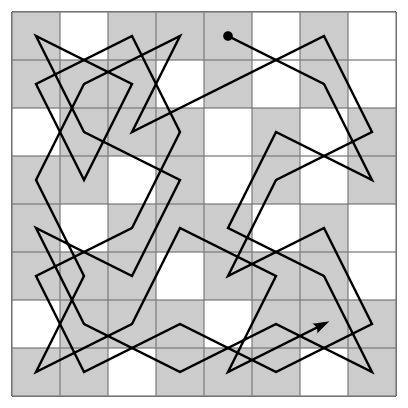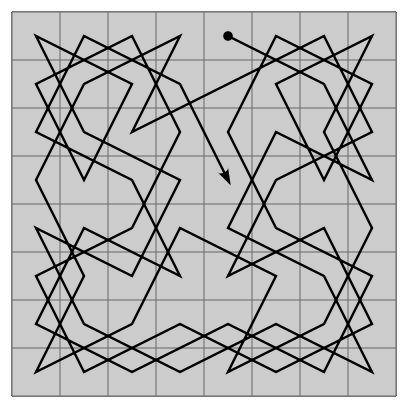
Knight's tour

A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square exactly once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is "closed", or "re-entrant"; otherwise, it is "open". The knight's tour problem is the mathematical problem of finding a knight's tour. Creating a program to find a knight's tour is a common problem given to computer science students. Variations of the knight's tour problem involve chessboards of different sizes than the usual 8 × 8, as well as irregular (non-rectangular) boards.

Tables

· History
vi (16)
vi (16)
sThi (1)
vi (16)
rA (30)
ha (19)
ga (9)
thA (2)
sAm (20)
ka (29)
sa (3)
tha (10)
dhA (24)
thA (27)
rA (11)
ma (4)
dhyA (26)
thA (23)
sa (31)
sa (31)
sThi (1)
sa (31)
rA (30)
thpA (8)
ga (9)
dhu (17)
sAm (20)
kE (14)
sa (3)
sa (21)
dhA (24)
rA (6)
rA (11)
sA (25)
dhyA (26)
mA (12)
ran (18)
ran (18)
sThi (1)
ran (18)
rA (30)
ga (15)
ga (9)
rA (32)
sAm (20)
ja (7)
sa (3)
pa (28)
dhA (24)
dha (13)
rA (11)
nna (22)
dhyA (26)
ya (5)
sThi (1)
rA (30)
ga (9)
sAm (20)
sa (3)
dhA (24)
rA (11)
dhyA (26)
vi (16)
ha (19)
thA (2)
ka (29)
tha (10)
thA (27)
ma (4)
thA (23)
sa (31)
thpA (8)
dhu (17)
kE (14)
sa (21)
rA (6)
sA (25)
mA (12)
ran (18)
ga (15)
rA (32)
ja (7)
pa (28)
dha (13)
nna (22)
ya (5)
· Number of tours
1
1
n
1
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
1
2
2
n
2
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
0
3
3
n
3
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
0
4
4
n
4
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
0
5
5
n
5
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
1,728
6
6
n
6
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
6,637,920
7
7
n
7
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
165,575,218,320
8
8
n
8
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
19,591,828,170,979,904
n
Number of directed tours (open and closed)on an n × n board(sequence A165134 in the OEIS)
1
1
2
0
3
0
4
0
5
1,728
6
6,637,920
7
165,575,218,320
8
19,591,828,170,979,904

References

  1. Knight's Tours and Zeta Functions
    https://scholarworks.sjsu.edu/etd_theses/4836/
  2. The Oxford Companion to Chess
  3. Java How To Program Fifth Edition
    https://archive.org/details/javahowtoprogram00deit_1/page/326
  4. Discrete Applied Mathematics
    https://doi.org/10.1016%2F0166-218X%2892%2900170-Q
  5. The Turk: the life and times of the famous eighteenth-century chess-playing machine
    https://archive.org/details/turklifetimesoff00stan/page/30
  6. Kavyalankara of Rudrata (Sanskrit text, with Hindi translation);
  7. www.iiitb.ac.in
    https://www.iiitb.ac.in/CSL/projects/paduka/paduka.html
  8. Bridge-India
    http://bridge-india.blogspot.com/2011/08/paduka-sahasram-by-vedanta-desika.html
  9. A History of Chess by Murray
  10. "MathWorld News: There Are No Magic Knight's Tours on the Chessboard"
    http://mathworld.wolfram.com/news/2003-08-06/magictours/
  11. Mathematics Magazine
    https://web.archive.org/web/20190526154119/https://pdfs.semanticscholar.org/c3f5/e69e771771de1be50a8a8bf2561804026d69.pdf
  12. Fibonacci Quarterly
    https://www.fq.math.ca/Scanned/16-3/cull.pdf
  13. "Knight's Tours on 3 by N Boards"
    https://www.mayhematics.com/t/oa.htm
  14. "Knight's Tours on 4 by N Boards"
    https://www.mayhematics.com/t/oc.htm
  15. Electronic Journal of Combinatorics
    https://doi.org/10.37236%2F1229
  16. Technical Report TR-CS-97-03
    https://web.archive.org/web/20130928001649/http://www.combinatorics.org/ojs/index.php/eljc/article/downloadSuppFile/v3i1r5/mckay
  17. Branching Programs and Binary Decision Diagrams
    https://books.google.com/books?id=-DZjVz9E4f8C&dq=532&pg=PA369
  18. MathWorld
    https://mathworld.wolfram.com/KnightGraph.html
  19. Evolutionary Optimization Algorithms
    https://books.google.com/books?id=gwUwIEPqk30C&pg=PA449
  20. Discrete Applied Mathematics
    https://core.ac.uk/download/pdf/81964499.pdf
  21. Communications of the ACM
    https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.412.8410
  22. GitHub
    https://github.com/douglassquirrel/warnsdorff/blob/master/5_Squirrel96.pdf?raw=true
  23. A Predictive Data Analytic for the Hardness of Hamiltonian Cycle Problem Instances
    https://pure.uva.nl/ws/files/30312375/_2018_Van_Horn_et_al_A_Predictive_Data_Analytic.pdf
  24. Finding Re-entrant Knight's Tours on N-by-M Boards
    https://doi.org/10.1145%2F503720.503806
  25. Century/Acorn User Book of Computer Puzzles
  26. Y. Takefuji, K. C. Lee. "Neural network computing for knight's tour problems." Neurocomputing, 4(5):249–254, 1992.
Image
Source: —
Tip: Wheel or +/− to zoom, drag to pan, Esc to close.